Capacidad de memoria
Última actualización: 2026-01-08 | Mejora esta página
Tiempo estimado: 12 minutos
Hoja de ruta
Preguntas
¿Qué impacto tiene la sobrecarga cognitiva en la capacidad de aprendizaje?
¿Cómo puede un mapa conceptual ayudar a evitar esa sobrecarga?
¿Qué técnicas docentes podemos usar para favorecer la comprensión sostenida?
Objetivos
Reconocer la relación entre la capacidad cognitiva y la carga de información.
Identificar estrategias para organizar el contenido sin saturar la memoria de trabajo.
Explorar el uso de mapas conceptuales como apoyo para construir estructuras de conocimiento.
Repaso de Mapas Conceptuales
Pregunta para responder por el chat: ¿Les pasó alguna vez estar en una clase en la que vienen entendiendo todo y luego de un rato pierden completamente el hilo y lo que venían entendiendo comienza a desvanecerse y la clase parece convertirse en un blablabla sin sentido? En esta presentación vamos a explorar un poco por qué podría pasar esto, y una posible razón está relacionada con el intervalo 7 más o menos 2.

Cuando presentamos los mapas conceptuales, dijimos que cada nodo/caja y cada relación/flecha cuenta como un ítem para retener en nuestra memoria de corto plazo o memoria de trabajo. También explicamos que la memoria de trabajo puede retener pocos ítems a la vez. En este mapa conceptual hay muchos más elementos de los que la memoria de corto plazo de la mayoría de las personas puede retener.
Una forma de abordar las limitaciones de la memoria de trabajo es dividir el mapa conceptual de contenidos a enseñar en partes, e incluyendo evaluaciones formativas después de cada parte. ¿Pero cómo? ¿Y qué tan grandes deben ser las partes en las que dividimos el mapa conceptual?
Para responder a esa pregunta, volvamos a nuestro diagrama de arquitectura cognitiva y echemos otro vistazo a la memoria a corto plazo. Aprovechemos para repasarlo también.
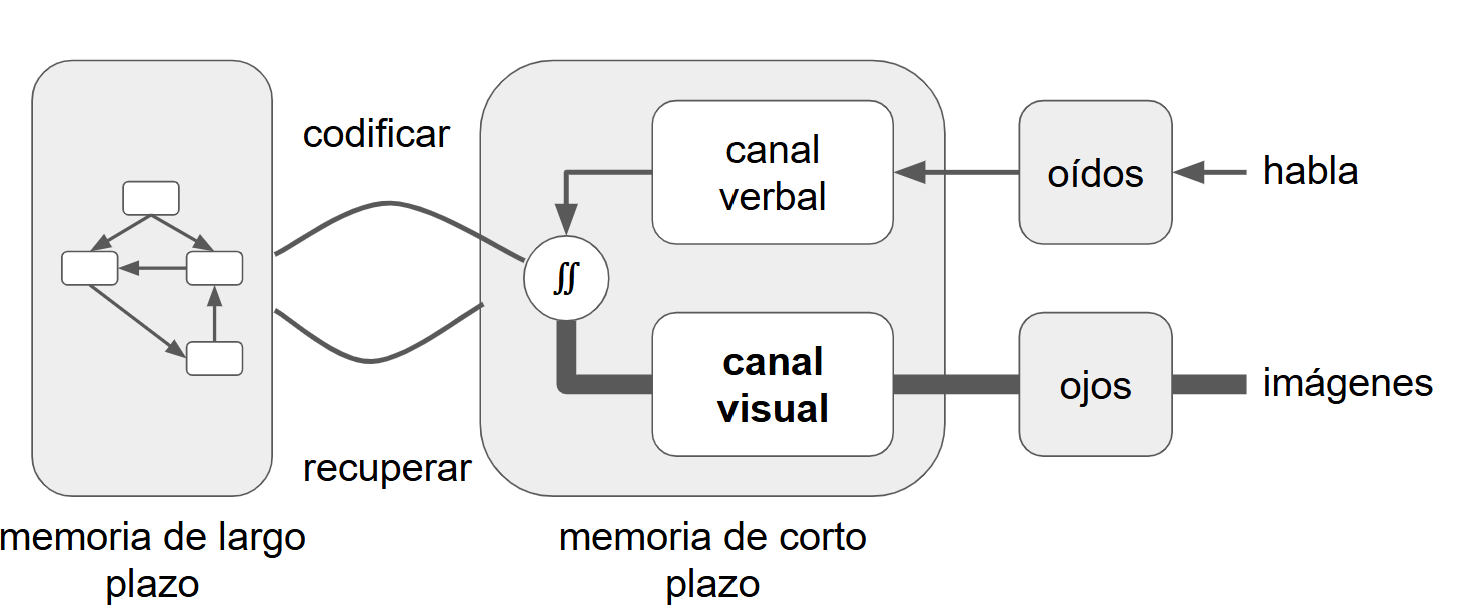
Siete Más o Menos Dos
Ya en la década de 1950, se comprobó que la persona promedio solo puede tener en la memoria a corto plazo unos pocos elementos a la vez. Las estimaciones iniciales ponen el número en 7 ± 2; estimaciones más recientes lo ponen tan bajo como 4.
7 más/menos 2 es una de las razones por las cuales, en la época en que se usaban estos teléfonos y recordábamos los números de memoria, los números de teléfono tenían entre 6 y 8 dígitos. Es difícil mantener más dígitos que eso en la memoria a corto plazo el tiempo suficiente para que el disco gire.
También puede ser la razón por la cual la unidad básica de la organización social humana es media docena de personas. Desde equipos deportivos y formaciones militares, pasando por círculos de tejido hasta reuniones, ese parece ser el límite de la cantidad de personas que pueden estar hablando o trabajando en conjunto al mismo tiempo. Más allá de eso, los grupos más grandes se dividen rápidamente en subgrupos. Si tienes 20 personas en una reunión, tienes tres reuniones en curso o una reunión de media docena de personas con un grupo de personas observando cómo se desarrolla la reunión.
Cuéntalos Todos
Volvamos una vez más a nuestro mapa conceptual de la fotosíntesis. Hay 9 nodos y 7 relaciones etiquetadas (algunas de las cuales son de uno a muchos nodos, pero lo ignoraremos por ahora). Eso hace un total de 16 cosas para que sus estudiantes absorban, y eso nos dice que esto es demasiado material para abordar de una vez.

Una porción factible de recordar puede ser:
“Durante la fotosíntesis se produce glucosa y se guarda como energía”
Otra porción puede ser:
“Durante la fotosíntesis se produce oxígeno que es liberado al aire”
Podemos usar el mapa conceptual para guiar nuestra elección del tamaño del fragmento y también los objetivos secundarios. Esto es un arte: la experiencia nos dictará qué segmentos funcionan mejor.
Pero, si la memoria a corto plazo solo puede contener media docena de cosas a la vez, ¿cómo podemos pensar en cosas más grandes? La respuesta es que si las cosas ocurren frecuentemente juntas, las almacenamos y las recuperamos en pedazos.
Ejercicio
Es puramente visual
En la próxima pantalla vamos a mostrar por 30 segundos los números del 1 al 9 asociados a un símbolo.
Usemos los 30 segundos para memorizar los símbolos.

Tienen 30 segundos para escribir sus números de teléfono usando los símbolos.
Pregunta para responder por el chat, ¿cuántos dígitos pudieron escribir usando el código?
Decíamos entonces que para pensar en cosas grandes, y que frecuentemente ocurren juntas, es más fácil si las almacenamos y las recuperamos en pedazos. Así que intentemos nuevamente el ejercicio.
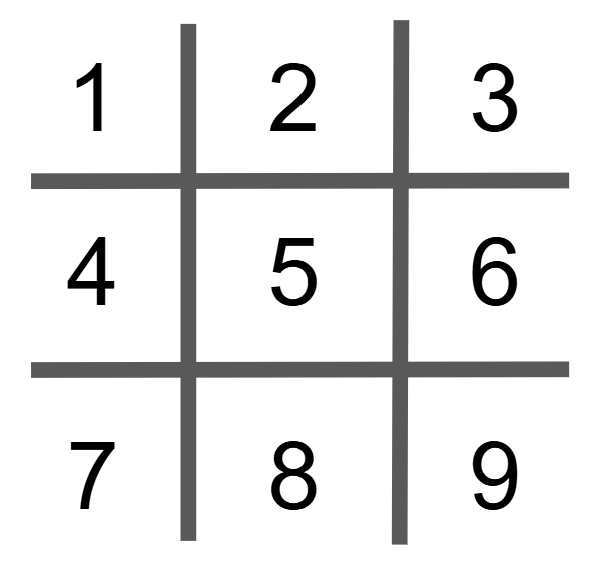
Esto es más fácil, ¿no? Nuestros cerebros son muy buenos para ver patrones. Tan buenos, de hecho, que verán patrones que no existen (¡como las caras en las nubes!). Como docentes, podemos usar esto para reducir la carga cognitiva y acelerar el aprendizaje.
Ejemplos desvanecidos
Cuando aprendemos una habilidad técnica, como resolver problemas matemáticos o escribir programas, suele ser muy útil comenzar con ejemplos completamente resueltos. Estos ejemplos permiten entender cómo se estructura una solución sin tener que tomar todas las decisiones al mismo tiempo. Desde el punto de vista de la carga cognitiva, esto es clave: la persona que aprende puede concentrarse en qué pasos se siguen y por qué, en lugar de tener que decidir simultáneamente la estrategia, el orden de los pasos y los detalles técnicos.
Sin embargo, si el aprendizaje se limita a observar soluciones completas, aparece un problema: se puede reconocer la solución cuando se la ve, pero no necesariamente reproducirla de manera autónoma. Para abordar esta dificultad, se utiliza la estrategia de ejemplos desvanecidos. Esta consiste en presentar una secuencia de ejercicios en los que la solución está inicialmente completa, pero en cada nuevo ejercicio se eliminan algunos pasos, de forma gradual y deliberada.
Por ejemplo, en matemáticas, al enseñar a resolver ecuaciones lineales, el primer ejemplo puede mostrar todos los pasos:
| Resolver: (4x + 8) / 2 = 5 |
|---|
| 4x + 8 = 10 |
| 4x = 2 |
| x = 1/2 |
En el siguiente ejercicio, se puede pedir a las personas que completen solo algunos pasos:
| Resolver: (2x + 8) / 4 = 1 |
|---|
| 2x + 8 = ___ |
| 2x = ___ |
| x = ___ |
Finalmente, se propone un ejercicio similar sin pasos intermedios, donde la persona debe aplicar por sí misma la estrategia aprendida. En este proceso, el desvanecimiento guía la atención hacia la estructura del procedimiento (aislar la incógnita, aplicar operaciones inversas) en lugar de hacia cada cálculo puntual.
Un proceso similar podemos aplicar en la programación. Supongamos que estamos enseñando a escribir una función que calcule el promedio de una lista de números. En un primer ejemplo, el código puede estar completamente desarrollado y comentado:
R
library(ggplot2)
ggplot(mtcars, aes(x = wt, y = mpg)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
Luego, en un ejemplo desvanecido, se puede presentar el mismo código con partes faltantes:
R
library(ggplot2)
ggplot(______, aes(x = ____, y = _____)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) R
library(ggplot2)
ggplot(_____, aes(x = ____, y = _____)) +
geom______() +
geom______(method = "lm", se = FALSE) Y, finalmente, pedir que escriban el código completo desde cero, tal vez incorporando otras variables o funciones. De esta manera, quienes aprenden no solo recuerdan líneas de código, sino que construyen un patrón reutilizable: en este caso la estructura para realizar un gráfico con r y ggplot2.
A continuación, vemos un ejemplo de ejemplos desvanecidos en Python. Primero, presentamos el ejemplo completo, donde se puede observar cómo se define una función, cómo se usan los parámetros y cómo se devuelve un valor:
PYTHON
def sumar_dos_numeros(a, b):
"""Suma dos números"""
return a + b
suma3_5 = sumar_dos_numeros(5, 3)
print(suma3_5)Luego, desvanecemos los parámetros y la expresión de retorno, para centrar la atención en qué información necesita la función para operar y qué valor produce:
PYTHON
def sumar_dos_numeros(____, ____):
"""Suma dos números"""
return _______
suma3_5 = sumar_dos_numeros(5, 3)
print(suma3_5)Finalmente, retiramos las palabras clave y las funciones principales, de modo que quienes aprenden deban reconstruir la estructura completa de la función y su uso, apoyándose en el patrón observado en los pasos anteriores:
PYTHON
____ sumar_dos_numeros(a, b):
"""Suma dos números"""
_____ a + b
suma3_5 = sumar_dos_numeros(5, 3)
_____(suma3_5)Los ejemplos desvanecidos funcionan como un andamiaje gradual: ofrecen mucho apoyo al comienzo y lo retiran progresivamente. Esto permite que las personas pasen de observar soluciones a pensar como quienes resuelven el problema, construyendo fragmentos y modelos mentales que luego pueden transferirse a nuevas situaciones.
Respecto de lo que hablamos en la unidad de carga cognitiva: ¿cómo les parece que ayudan este tipo de ejercicios?
Desde la perspectiva de la carga cognitiva, los ejemplos desvanecidos reducen la carga extrínseca (no es necesario decidir todo al mismo tiempo) y favorecen la carga pertinente, es decir, el esfuerzo mental que realmente contribuye al aprendizaje. Además, al invitar a completar pasos faltantes, fomentan la autoexplicación, que fortalece la codificación en la memoria de largo plazo.
Ejercicio
Escriban un procedimiento de 4 a 5 pasos cortos de algo que podrías enseñar.
Reemplacen 2 a 3 elementos con ______
Expliquen: ¿A qué estamos llamando la atención en su elección de qué se desvanece?
###Pausa
No se desconecten, pero sí aléjense de pantallas.
Volvemos en 10 minutos.
Resumen hasta aquí
Este mapa conceptual sintetiza varios de los conceptos vistos hasta el momento. Particularmente, cómo el aprendizaje está condicionado por una capacidad cognitiva limitada y cómo el diseño didáctico puede acompañar esa realidad. Al representar modelos mentales, los mapas conceptuales nos ayudan a diseñar lecciones que se ajusten a la memoria de corto plazo, reduzcan la carga cognitiva y favorezcan la construcción de conocimiento duradero. Estrategias como la fragmentación permiten ampliar efectivamente lo que podemos procesar, facilitando la codificación en la memoria de largo plazo y la formación de nuevos modelos mentales. En definitiva, enseñar bien no es decir más, sino organizar mejor.
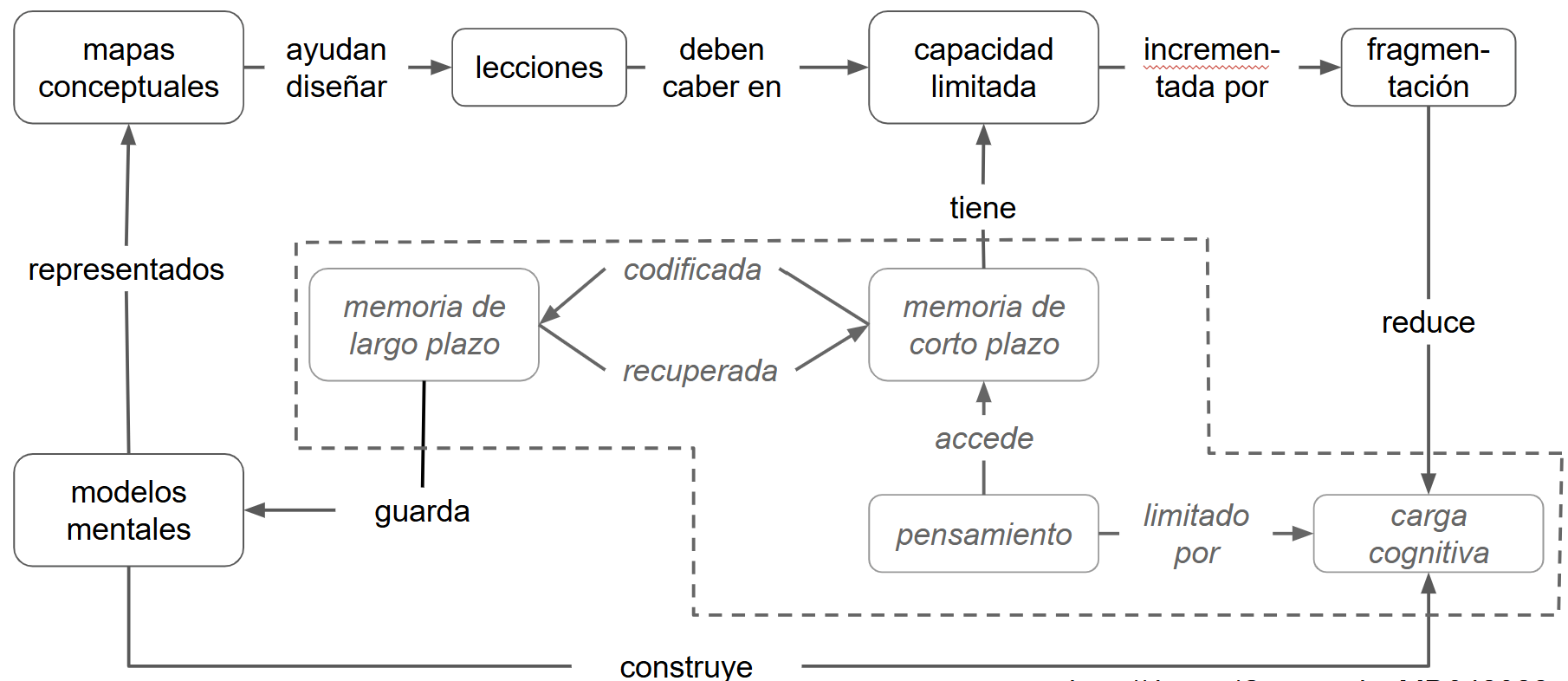
La memoria de trabajo tiene una capacidad limitada, y cuando se la sobrecarga, la comprensión se deteriora rápidamente.
En un mapa conceptual, cada concepto y cada relación cuentan como ítems que consumen capacidad cognitiva.
Fragmentar el contenido en porciones pequeñas y manejables reduce la carga cognitiva y mejora el aprendizaje.
El reconocimiento de patrones y la construcción de “fragmentos” permiten pensar y aprender cosas más complejas.
Estrategias como los mapas conceptuales y los ejemplos desvanecidos ayudan a diseñar lecciones alineadas con cómo funciona la cognición humana.
